基于BASE32的兑换码生成算法详解
Cite:来源于黑马程序员-天机学堂,该算法基于BASE32算法与JWT的加密思想。
需求分析
对于优惠券兑换码,具有以下需求:
- 可读性强:设想,你拿到一个兑换码,其中既含有I、又含有1(或是既含有O、又含有0,对于某些无法区分这两者的字体,读者体验感会大大降低!
- 数据量大:兑换码的需求量往往是很大的,毕竟给使用者发放兑换码可以促进消费,且不带来什么损失。同时,考虑到未来可能的需求,也要求算法所能生成的兑换码数据量是千万乃至亿级。(总之,越大越好~)
- 不可重兑:这算是硬性要求了!如果不能根据兑换码来判断是否使用过,那么对商家的损失就太大了。
- 防止爆刷:这也是硬性要求!!设想,你的兑换码生成算法被有心者破译,那么利用某些无门槛券来购买某些商品,甚至出售兑换码,那么造成的损失是不可估量的!
- 效率高:兑换码生成和校验必须是高效率的。
算法分析
基本算法
基于需求分析,我们来逐步拆解兑换码生成算法。
考虑到不可使用I1、O0,那么可以使用的字符为:A~Z中的24个字母、0~9中的8个数字,一共32个字符可使用。而$2^5=32$,那我们就可以用一个5位二进制数来表示1个字符,而为了满足”数据量大“的要求,我们可以使用一个32位的二进制数!这样,一个32位的二进制数就可以生成 个兑换码!基本可以满足大部分应用场景了!
个兑换码!基本可以满足大部分应用场景了!
但是,到这也只是完成了“数据量大”和“可读性强”这两个要求!剩下两个呢?
考虑到需要快速判断,所以将兑换码记录插入数据库,并以兑换码(作为主键或者字段)是否存在来判断是否被兑换过,肯定是不可行的! 这里不可行主要有两点:①频繁查询数据库(?);②兑换码太多,对数据库存储压力大!
所以,我们采用使用Redis中的BITMAP来进行兑换码的快速校验!同时,兑换码的生成采用自增ID,这样就可以通过INCR NUMS指令来实现高效的兑换码生成,以及基于BITMAP的SET BIT OFFSET快速判断。
到这里,我们已经完成4个需求了,还剩下最后一个:防止爆刷,也就是加密过程。
加密算法
目前,我们的兑换码还是一个32位的二进制数字。我们参考JWT的设计思想:
- JWT由
Header-PayLoad-Signature构成,其中Signature就是根据Header与PayLoad生成的!因此,只要后台的密钥与签名算法不泄露,即使黑客更改Header与PayLoad,后台根据篡改后的Header与PayLoader与篡改后的Signature也对不上。
所以,我们根据32位的二进制数字与JWT的加密思想,对兑换码进行加密处理。
我们定义两个结构:①新鲜值;②密钥。其中,新鲜值对应Header,用来存储签名算法;密钥对应Signature,是利用新鲜值与32位数字生成的。
新鲜值
新鲜值我们在这定义为4位二进制数字,根据32位数字的后4位生成。利用此新鲜值对应不同的16种加密算法。
密钥
根据新鲜值,我们可以定义16种加密算法:
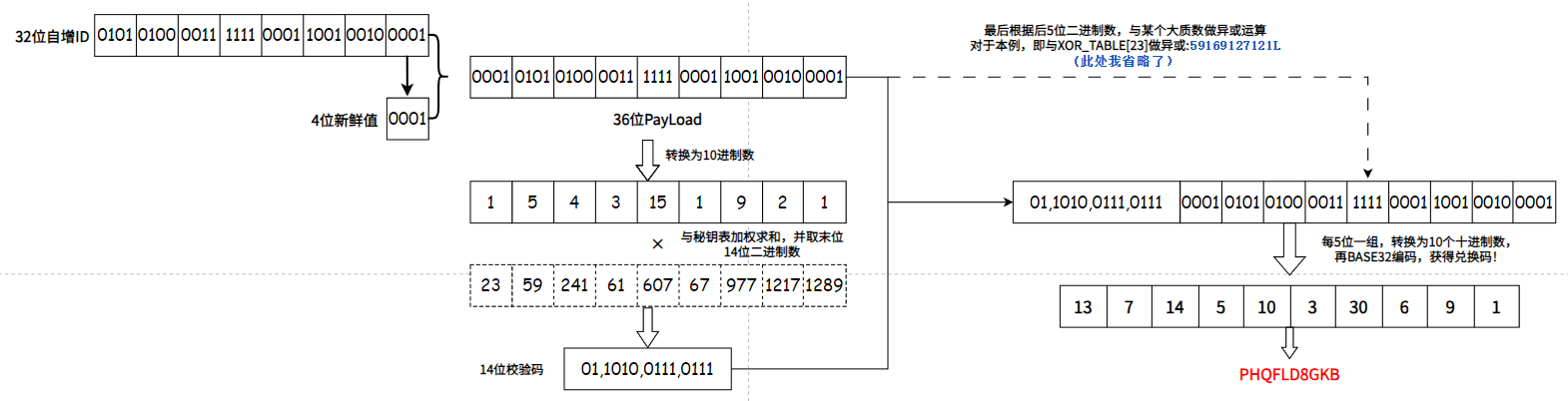
- 将PayLoad与新鲜值进行拼接,获取36位二进制数字;
- 将36位数字转换为9位数字,与加权数进行相乘求和,并对$2^{14}$求模,以便能转换为14位二进制数字,与36位数字拼接;
- 获取14位二进制数后,截取其后5位二进制数,与转换为10进制后对应的大质数进行异或,以进一步混淆秘钥。
最后,我们将PayLoad+新鲜值+密钥拼接,就可以得到50位二进制数,以每5位为一组转换为10进制数,就可以对应32位字符中的一个。
总结
到这里,我们已成功完成兑换码的生成,总结一下5个要求是否都满足:
- 可读性强:由A~Z、0~9(排除IO10)的32位字符中的10位组成。
- 数据量大:基于32位自增ID生成,可以满足40亿量级的兑换码数量!
- 不可重兑:基于BITMAP进行兑换码是否兑换的判断。
- 防止爆刷:参考JWT的设计思想进行了加密设计,只要后台秘钥与加密算法不泄露,就是安全的。
- 效率高:基于BITMAP的自增ID进行生成与校验,高效。